El cerebro es el órgano encargado de la coordinación del funcionamiento de un organismo a través de la entrada, procesamiento y el envío de información por medio de las neuronas. Las neuronas se comunican utilizando señales eléctricas y químicas. Las señales eléctricas llamadas potenciales de acción se generan por el movimiento de iones dentro y fuera de la membrana de la neurona, pero esta señal eléctrica no es capaz de atravesar el espacio entre dos neuronas, es por medio de la liberación de sustancias químicas llamadas neurotransmisores que permiten la comunicación entre dos neuronas o entre neurona y el tejido del cuerpo. La neurociencia es la encargada del estudio del cerebro y en general, del sistema nervioso, pero otras ciencias como la fisiología, la química, la biofísica, la matemática entre otras, han contribuido en el estudio de este órgano.

Los primeros escritos en papiros egipcios donde se utilizan matemáticas o donde aparece la palabra cerebro para describir síntomas y diagnósticos de pacientes datan del siglo XVII al XX a. C. Aquí se verá como las matemáticas han contribuido al desarrollo de la neurociencia. La ciencia que estudia la aplicación de modelos matemáticos y métodos computacionales para entender el sistema nervioso recibe el nombre de neurociencia teórica (o neurociencia computacional). Los modelos matemáticos utilizados para estudiar el sistema nervioso se clasifican en dos grupos: modelos de redes de neuronas y modelos de neuronas únicas (Kandel y cols., 2013:1602).

Los modelos de redes o de circuitos neurales, han sido utilizados para contestar preguntas de procesos complejos que involucran un conjunto de neuronas, por ejemplo; ¿cómo las neuronas de ciertas áreas del cerebro permiten que percibamos hambre?, ¿cómo los circuitos neurales permiten que clasifiquemos objetos o recordemos sucesos de nuestra niñez?, ¿cómo la integración de información puede ayudarnos a tomar decisiones? Los modelos matemáticos han contribuido a responder a estas interrogantes.

Los modelos de neuronas únicas son utilizados para contestar preguntas más específicas de las neuronas. Por ejemplo, ¿qué tanto afecta al patrón de actividad de una neurona si se le aplican diferentes estímulos como electricidad o sustancias químicas?, ¿cómo la morfología (forma) de las neuronas puede modificar su funcionamiento? Se ha propuesto estudiar la plasticidad sináptica con el uso de modelos de neuronas únicas en donde se utiliza la “propagación hacia atrás” para enviar información a las sinapsis (Kandel, 2021).

El modelo matemático de neurona única que quizás es el más representativo fue propuesto por los fisiólogos Andrew Fielding Huxley y Alan Lloyd Hodgkin. Ellos realizaron una serie de estudios utilizando el axón gigante del calamar para estudiar la excitación e inhibición de la neurona, y les permitió registrar el potencial de acción, y clasificar la corriente iónica en dos componentes, en una corriente rápida y otra lenta, generadas por la entrada de sodio y salida de potasio de la neurona, respectivamente. Su conocimiento del modelado de circuitos eléctricos con ecuaciones diferenciales les permitió interpretar a la neurona como un circuito eléctrico básico (capacitor, resistencia y fuente) y modelarlo con un sistema de ecuaciones diferenciales (Hodgkin y Huxley, 1952). La importancia de estos estudios permitió que Huxley y Hodgkin (H&H) fueran acreedores al premio nobel de medicina y fisiología en 1963.

Los experimentos realizados por H&H formaron las bases para el estudio eléctrico de las neuronas, y motivó al descubrimiento de los canales implicados en la generación de potenciales de acción. A continuación, se describen algunos puntos de como este modelo impulsó el estudio de la neurona tanto estructuralmente como en su funcionamiento:

Impulsó el desarrollo de la técnica llamada fijación de voltaje (voltage clamp), ya que utilizaron un electrodo dual evitando problemas de polarización. El uso de la fijación de voltaje permitió que H&H registraran corrientes de iones a través de la membrana del axón gigante del calamar.

El modelo sirvió como base para que Neher y Sakman desarrollaran la técnica de Patch-clamp y más tarde compartieran el premio Nobel en 1991 por el descubrimiento del funcionamiento de canales iónicos aislados.

En 2003 MacKinnon recibió el premio nobel por la descripción de la estructura de los canales iónicos. La estructura descrita por MacKinnon corroboró el porqué de algunos términos del modelo de H&H. Este es un claro ejemplo de cómo los modelos matemáticos teóricamente pueden revelar mecanismos biológicos subyacentes antes de ser descubiertos experimentalmente.

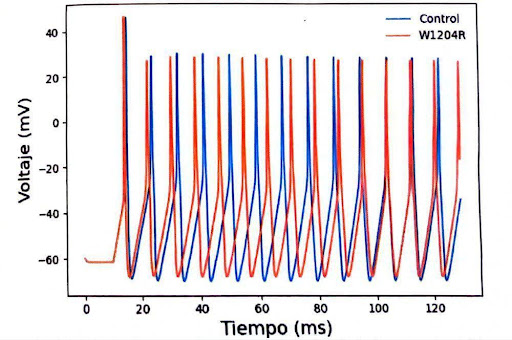
El modelo de H&H ha sido utilizado para estudiar las propiedades eléctricas de neuronas y su relación con enfermedades nerviosas. En específico, ha sido ampliamente utilizado para estudiar la epilepsia. Los resultados del modelo propuesto por Mendoza y cols., que es una modificación al modelo de H&H muestran que una neurona con una mutación que simula esta enfermedad se activa aun cuando los estímulos son de baja intensidad (Figura 1, López y cols., 2023), esto es característico de las personas que sufren epilepsia que bajo estímulos como la luz o sonido pueden desencadenar una convulsión.

El modelo de H&H ha sido modificado para estar más acorde a la estructura del axón de las neuronas, y a través del paso del tiempo se han utilizado diferentes herramientas matemáticas para complementar su análisis, entre las herramientas más recientes está el uso del cálculo fraccionario, (Miller y Ross, 1993; Nagy y Sweilam, 2014). El modelo de H&H se describe matemáticamente usando un sistema de ecuaciones diferenciales de orden 1, como las que se estudian a nivel medio superior. Bajo la óptica del cálculo fraccionario, el cambio que se hace a las ecuaciones del modelo es sustituir las derivadas enteras por derivadas decimales (fraccionarias). Este nuevo enfoque incluye el retardo en el tiempo que involucran la mayoría de los fenómenos biológicos. Los resultados numéricos de este nuevo enfoque han mostrado estar acorde a los resultados utilizando derivadas de orden entero (Nagy y Sweilam, 2014).

Un modelo teórico nunca logrará capturar todos los detalles de un fenómeno biológico y no necesariamente uno más detallado es mejor, en realidad, un modelo es adecuado si este permite representar el fenómeno biológico de manera simple, el ejemplo más representativo es el modelo de H&H. Cuando las neurociencias experimentales corroboran las hipótesis previstas por la neurociencia teórica se podrá refinar los modelos matemáticos, generando un círculo de colaboración entre ambas áreas.